Decibel scale

Reference : https://ccrma.stanford.edu/~jos/st/Properties_DB_Scales.html
https://ccrma.stanford.edu/~jos/st/Decibels.html 

A decibel (abbreviated dB) is defined as one tenth of a bel.

The bel is an amplitude unit defined for sound as the log (base 10) of the intensity relative to some reference intensity, i.e., 

     

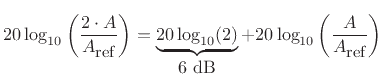
The choice of reference intensity (or power) defines the particular choice of dB scale. Signal intensity, power, and energy are always proportional to the square of the signal amplitude. Thus, we can always translate these energy-related measures into squared amplitude:

  

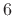
Since there are 10 decibels to a bel, we also have 

 

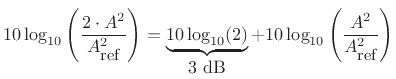
In every kind of dB, a factor of 10 in amplitude increase corresponds to a 20 dB boost (increase by 20 dB):

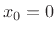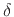A function which is proportional to is said to ``fall off'' (or ``roll off'') at the rate of 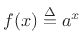dB per decade. That is, for every factor of 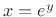in 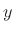(every ``decade''), the amplitude drops 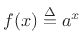dB.   

Similarly, a factor of 2 in amplitude gain corresponds to a 6 dB boost:

and

   dB 

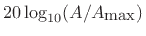
A function 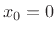which is proportional to 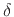is said to fall off 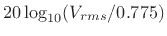dB per octave. That is, for every factor of 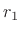in 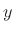(every ``octave''), the amplitude drops close to 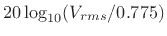dB. Thus, 6 dB per octave is the same thing as 20 dB per decade.  

A doubling of power corresponds to a 3 dB boost:

and 

dB